Positional encodings are a key component of Transformers for language modeling. Over time, multiple approaches have been proposed to incorporate sequence position into the model. To better understand the different approaches, I created a couple synthetic datasets and a small transformer decoder model to test different positional encodings. In this blog, I will walk through the sinusoidal positional encoding used in the original Transformer paper, as well as other variations such as RoPE, learned positional encodings, and even no positional encodings at all.
Experiment Setup
The analysis is performed on two simple synthetic datasets, with the vocabulary being uppercase English characters. The datasets are generated to test the model's ability to learn about the position of the tokens in the sequence. All sequences are 32 tokens long so that experiments can run quickly on a CPU.
- ShiftK: Each sample is formed by random characters, with the target at position i being the character at position i - k. This tests the model's ability to look back at previous tokens. In the experiments we use k = 4. For the first k tokens, the loss is not backpropagated.
- AlternatingChar: Each sample is formed by picking two distinct uppercase characters and alternating them for the entire sequence, e.g., ABABAB..., GZGZGZ..., etc.
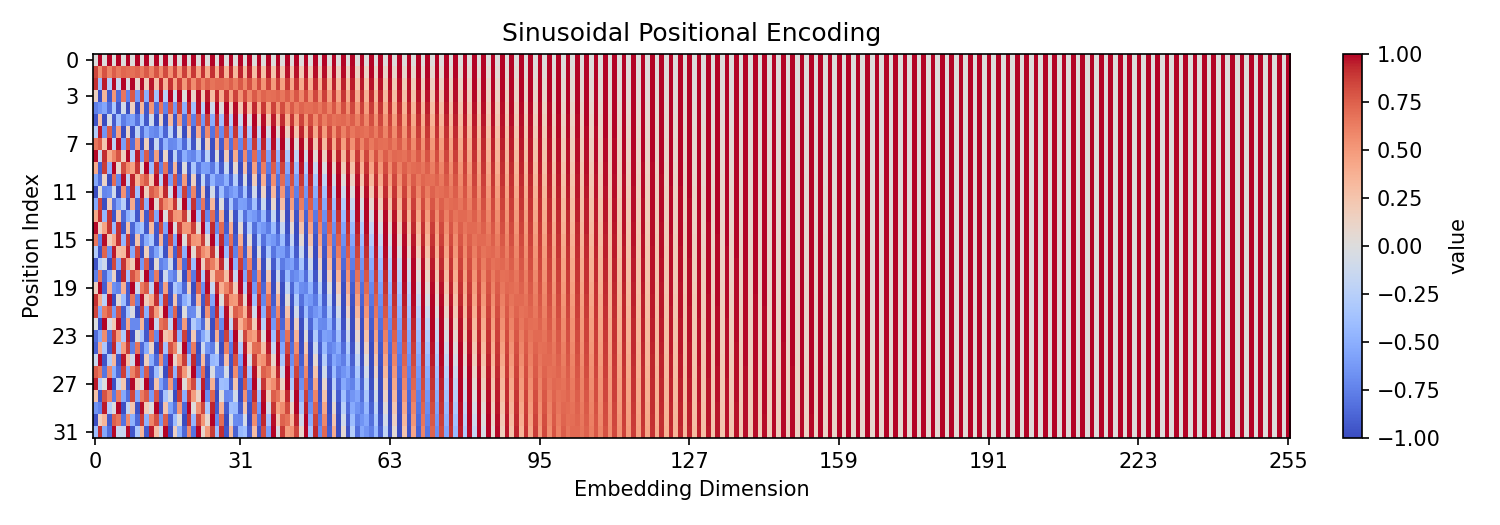
Sinusoidal Positional Encoding
The sinusoidal positional encoding used in the original Transformer paper is defined below, where \(PE(pos, i)\) is the positional encoding for position
\(pos\) and dimension \(i\). The positional encoding is added to the token embedding as input to the transformer.
$$
PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d}}\right)
$$
$$
PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d}}\right)
$$
An intuitive way to think about this is that each position gets a unique combination of sines and cosines at different frequencies.
Low frequency components allow the model to learn long-range patterns, while high frequency components allow it to learn short-range patterns.
The reason why both sine and cosine are used is because at a specific frequency \(\omega\), shifting position is equivalent to applying a linear rotation matrix.
For frequency \(\omega\), the encoding of position \(p\) is
\[
\begin{bmatrix}
\sin(\omega p) \\
\cos(\omega p)
\end{bmatrix}.
\]
Shifting by \(k\) gives
\[
\begin{bmatrix}
\sin(\omega (p+k)) \\
\cos(\omega (p+k))
\end{bmatrix}
=
\begin{bmatrix}
\cos(\omega k) & \sin(\omega k) \\
-\sin(\omega k) & \cos(\omega k)
\end{bmatrix}
\begin{bmatrix}
\sin(\omega p) \\
\cos(\omega p)
\end{bmatrix},
\]
so a shift corresponds to a fixed rotation in the 2D plane formed by the sine and cosine components for that frequency \(\omega\).
The fact that shifts are linear transformations allows the self-attention mechanism to efficiently utilize positional information.
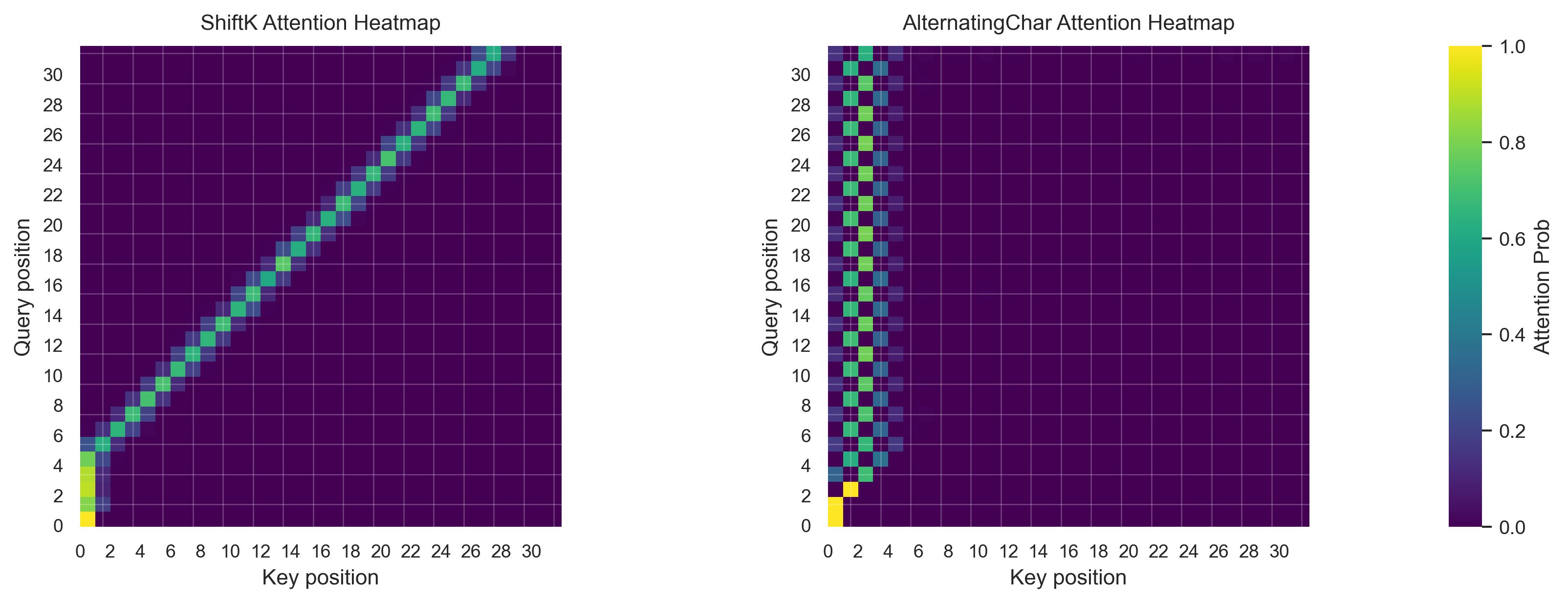
RoPE
Rotary Positional Embedding (RoPE) is similar to the sinusoidal positional encoding, but instead of adding the positional encoding to the token embedding, RoPE rotates the queries and keys in the self-attention mechanism according to their positions. For frequency \(\omega\), the rotation applied to position \(p\) is: \[ R_\omega(p) = \begin{bmatrix} \cos(\omega p) & \sin(\omega p) \\ -\sin(\omega p) & \cos(\omega p) \end{bmatrix}. \] In self-attention, the query and key vectors for position \(p\) are rotated: \[ q_p \gets R_\omega(p) \, q_p, \quad k_p \gets R_\omega(p) \, k_p. \] The attention score between positions \(p\) and \(q\) then becomes: \[ q_p^\top k_q = q_p^\top R_\omega(p)^\top R_\omega(q) k_q = q_p^\top R_\omega(q - p) k_q. \] This means the positional effect depends only on the relative distance \(q - p\), not the absolute positions. This has two important consequences:
- Pure relative position dependence: The positional factor \(R(q-p)\) depends only on the relative offset between tokens, enabling generalization to sequence lengths beyond training.
- Separation of concerns: Token embeddings carry purely semantic information, while positional relationships are injected only when computing attention scores. This avoids the content-position cross-terms present in the original sinusoidal approach, making relative position reasoning more direct.
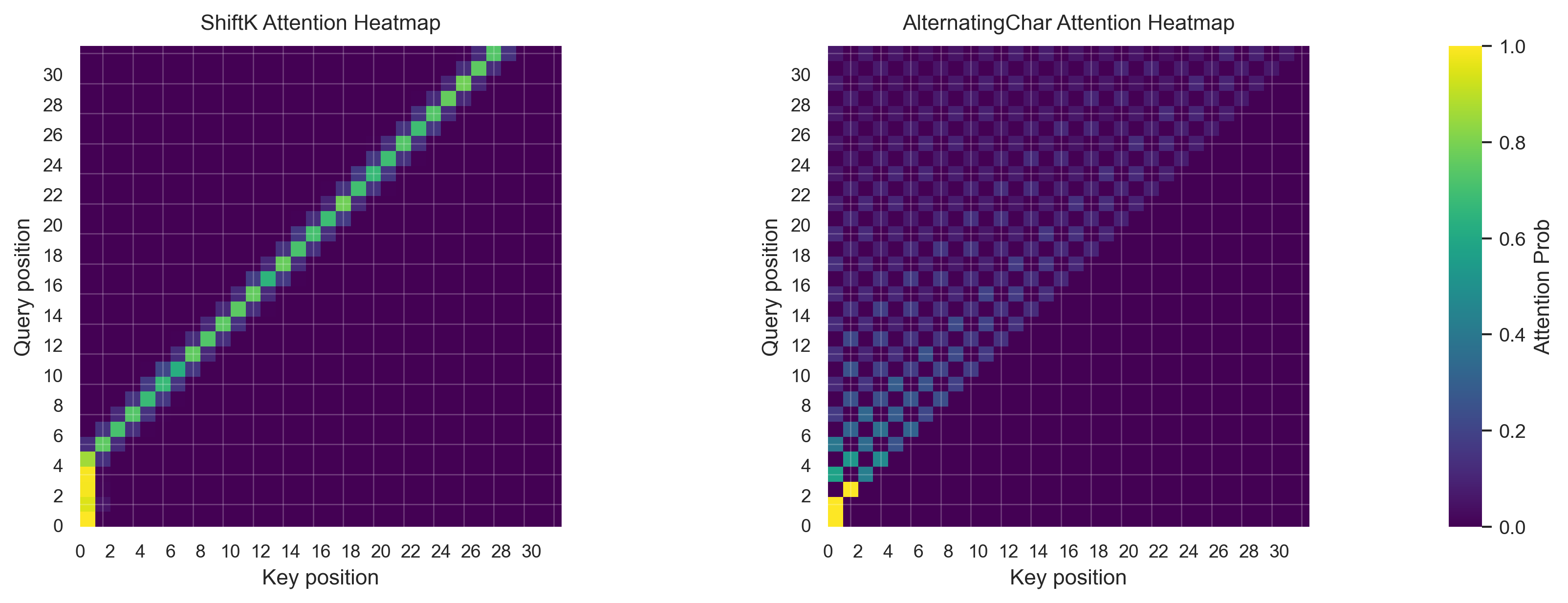
Learned Positional Encoding
Learned positional encodings are conceptually simple and do not involve any trigonometric functions.
There is a learnable embedding for each position which is added to the token embedding and learned via backpropagation.
In the original transformer paper, the authors claimed that they tried learned positional encodings and found similar
performance to the sinusoidal positional encoding. Ultimately they chose the sinusoidal positional encoding because it
allows for better generalization to longer sequences.
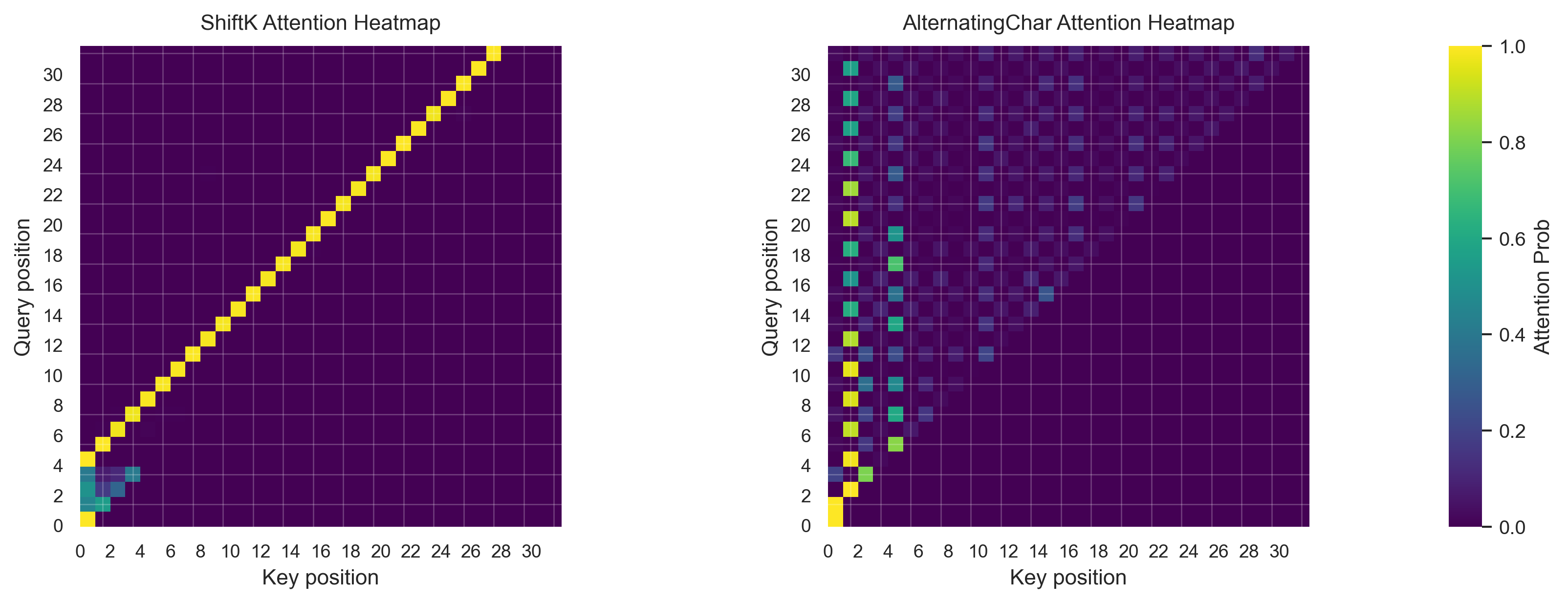
No Positional Encoding
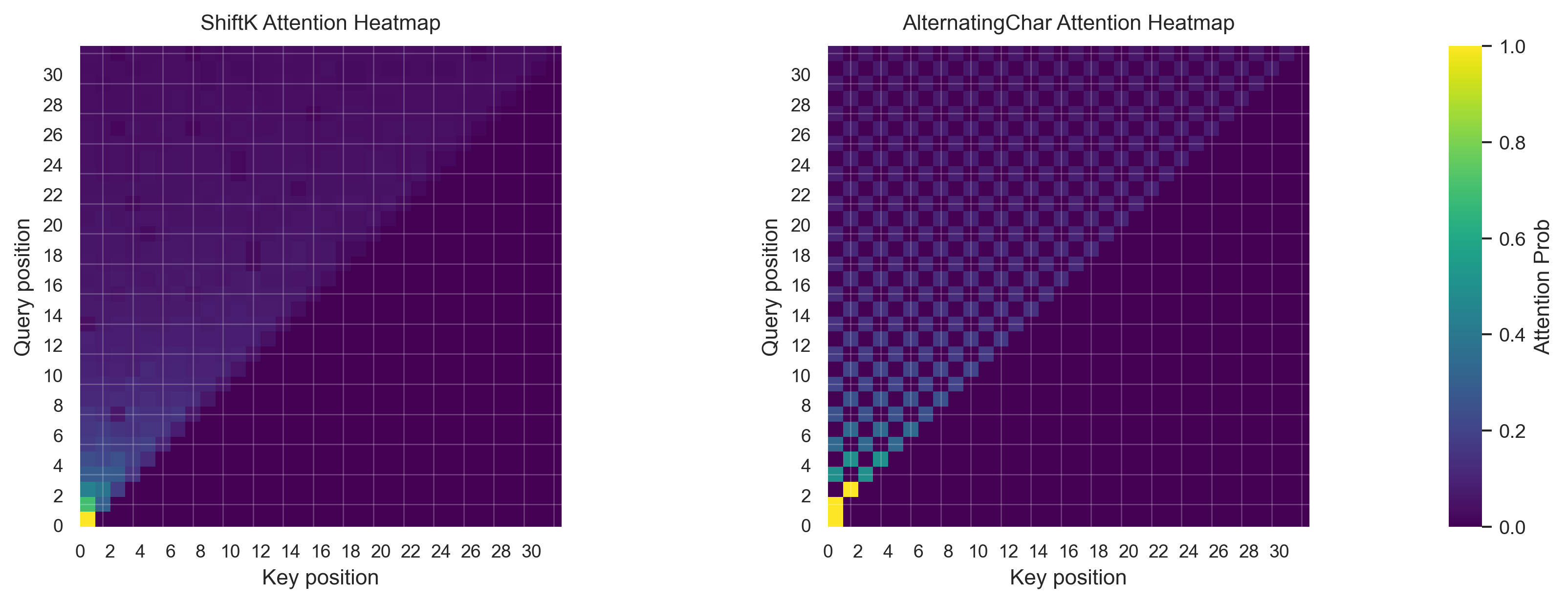
Lastly, we can use no positional encodings at all! This is inspired by the NoPE paper, which shows that
transformer decoder models can learn positional information via the causal mask implicitly. With my one layer transformer model,
I found the accuracy to only be 17% for the ShiftK dataset, but 96% for the AlternatingChar task.
However, 17% is still far better than random guessing (which would be around 4%).
Conclusion
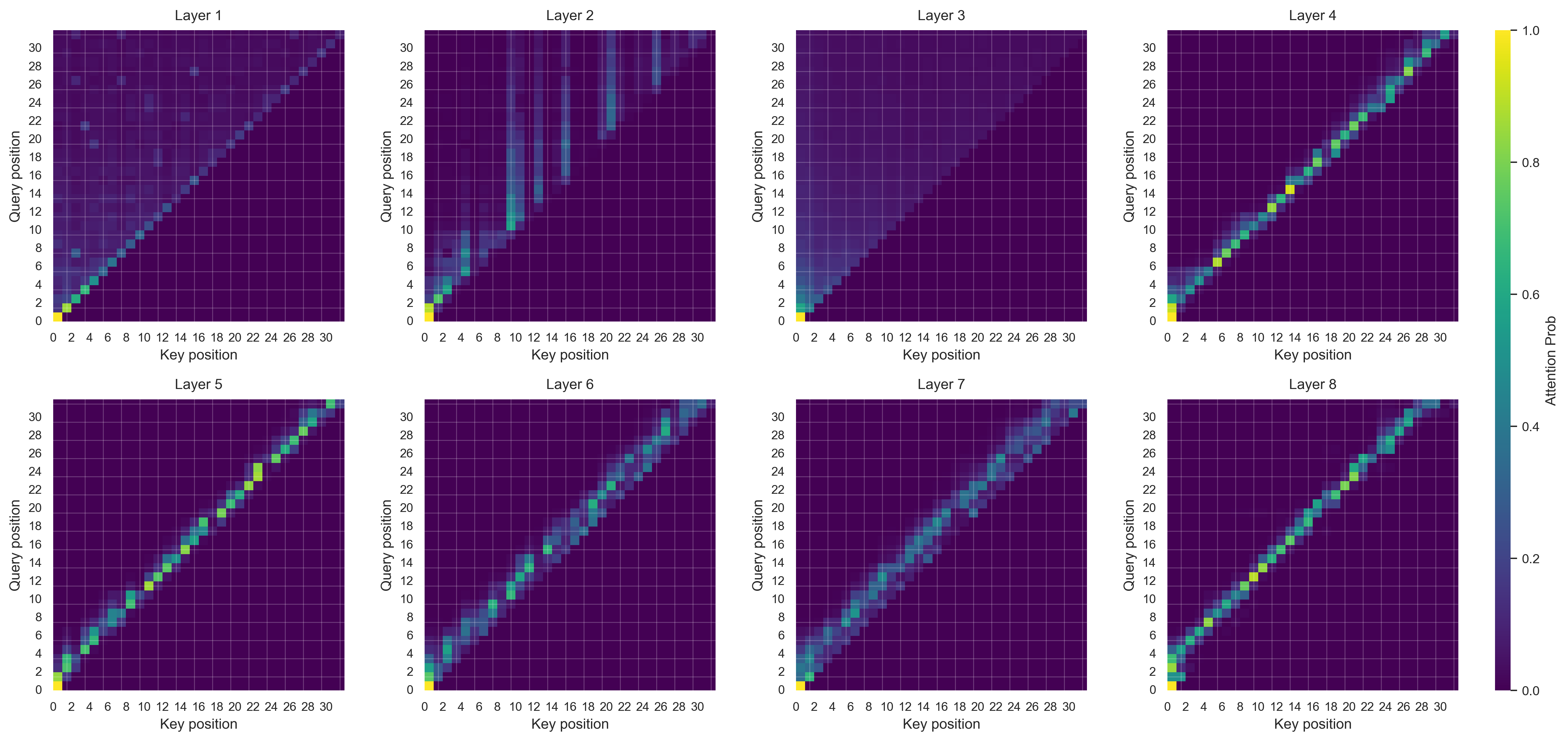
In this blog, we experimented with different positional encodings on a small transformer model with two synthetic datasets. The synthetic datasets were constructed to test the model's ability to utilize positional information. By analyzing the attention heatmaps, we were able to draw some insights into how the different positional encodings affect model learning.